Categoria de matemàtiques
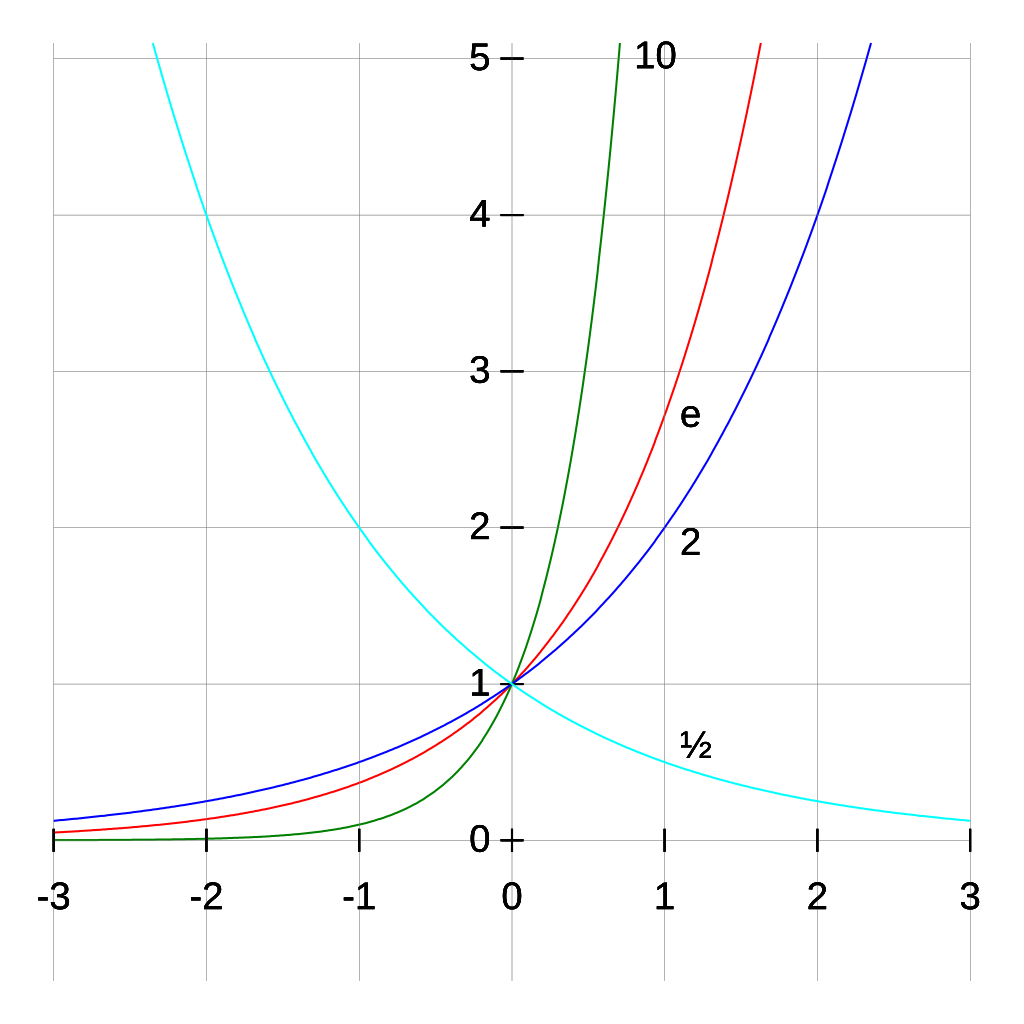
La potenciació és una operació matemàtica denotada per bn que comprèn l'ús de dos nombres, la base b i l'exponent (o potència) n. Quan n és un enter positiu, la potenciació correspon a una multiplicació repetida; en altres paraules, equival al producte de n factors, cadascun dels quals és igual a b:
Es pot fer l'analogia amb la multiplicació: quan es multiplica un nombre per un enter positiu, l'operació correspon a una suma repetida:
L'exponent se sol escriure en forma de superíndex a la dreta de la base. La potenciació bn es pot llegir de les següents maneres: «b elevat a n», «b elevat a la n-èsima potència» o, de manera curta, «b a la n». Alguns exponents tenen la seva pròpia pronunciació: per exemple, b² es llegeix «b al quadrat» i b3 es llegeix «b al cub».
La potència bn també es pot definir quan n és un enter negatiu, per una base b diferent de zero. No existeix cap extensió natural per tots els b i n reals, però quan la base b és un nombre real positiu, bn es pot definir per tots els exponents n reals i fins i tot complexos mitjançant la funció exponencial ez. Les funcions trigonomètriques es poden expressar en termes de potenciació complexa.T
La potenciació en la qual l'exponent és una matriu s'utilitza per resoldre sistemes d'equacions diferencials lineals.
La potenciació es fa servir a bastament en molts camps, entre els quals l'economia, la biologia, la química, la física i la informàtica, i té aplicacions tan diverses com l'interès compost, el creixement de la població, la cinètica química de reaccions, el comportament d'ones i la criptografia de clau pública.
- profesor: Carlo Bisconti Arias de Saavedra
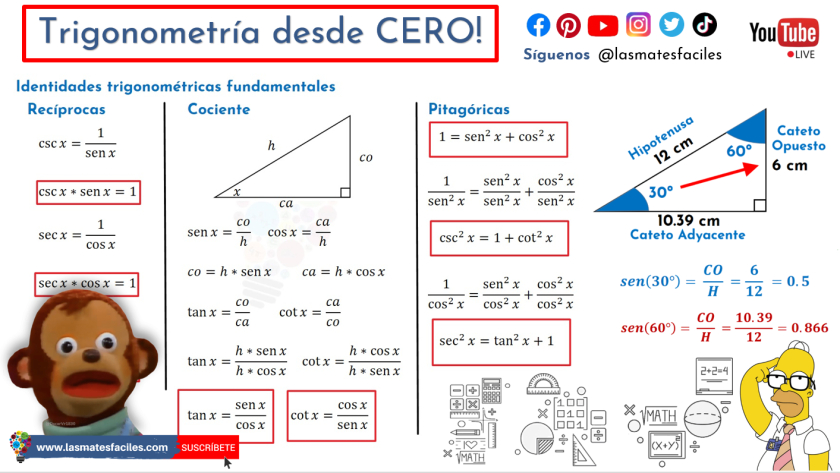
La trigonometria (del grec: "la mesura de triangles") és una branca de les matemàtiques que tracta les relacions internes dels triangles. Té relació directa amb la geometria, sent una de les bases de la geometria analítica. Les magnituds essencials que s'utilitzen són la distància i l'angle.
Té moltes aplicacions: la tècnica de la triangulació s'usa en astronomia per a mesurar la distància a estels propers, en topografia per a fer mapes i en sistemes de navegació per satèl·lit.
La branca de la trigonometria anomenada trigonometria esfèrica estudia els triangles que es dibuixen sobre esferes.
- profesor: Carlo Bisconti Arias de Saavedra

